Singapore Mental Math (4) – adding a series of odd numbers

Do read the previous few blog entries (here) to see the background to this.

This is the strategy for Week 1 in Grade 7 (which I assume is equivalent to Year 8 in England).

Good: Pupils will be following an algorithm and are using vocabulary, while also doing some mental maths.

Bad: Pupils might assume that in general all ‘series’ must start with 1.  It wasn’t made clear that for this algorithm to work it must start at 1.

Missed opportunity:

Why not mention that the answer is a square number?  (Step 3 could easily be: “Square the quotient obtained in Step 2”)

Why not explore why this is a square number?  There are so many ways to do this.  Here are a few I can think of immediately.]

 If there are an odd number of terms we can use the method from my previous post.  With 1 + 3 + 5 + 7 + 9 the middle number is 5 and there are 5 numbers.  The sum is therefore 5 squared.

The same is true for any odd number.

For an even number of terms we can still use the method from the previous post.  With 1 + 3 + 5 + 7 + 9 + 11 there are 6 terms and the middle is (1+11)/2= 6.  The sum is 6 squared.

Ah: so the algorithm is really adding the first and last terms, dividing by 2 and then squaring it.

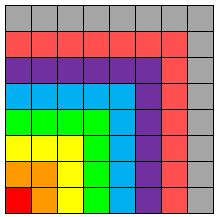
We could also draw a picture:

Each colour shows a successive odd number, and after each new colour has been added it is still a square.

We can also explore further why this pattern must increase by an extra 2 each time.  If we just add on the same amount as last time, this is what happens:

To fill those gaps we need to add on an extra 2.