Here’s another article that tries to show some calculations
but ends up being distant from the genuine mathematics. And the source data is, in some ways, even funnier.
This blog starts with a filleted version of the article. (The link is provided so you can see the
whole thing, but none of the mathematical info has been removed from my version.)
Plans to reopen shops in England
'in chaos' over social distancing rules
Study finds 10 sq metres of space is required per
shopper to stick to government’s 2-metre guidelines
Fri 5 Jun
2020 14.19
High street retailers
must give each shopper a minimum of 10 sq metres of space if they are to
maintain social distancing rules, a new study has found, prompting businesses
to complain that a lack of official guidance has left reopening plans in chaos.
With 10 days to go
until most non-essential shops reopen in England, a research paper by Manchester Metropolitan and Cardiff univeristies has
concluded that larger shops must allow substantially more than a 2-metre radius
for each person so that they can move freely.
The study finds
that people need 10 sq metres in smaller shops, 11 sq metres in larger shops,
and 12 sq metres in outdoor spaces where they move more rapidly. That is up to
three times as much space as the 2-metre radius required when people are
stationary.
The report’s
conclusions are based on the speed and unpredictability of people’s movements,
which means they are much more likely to get near each other when shopping than
when queuing or sitting at a desk – and therefore require a bigger “halo”.
Chris Turner, the
chief executive of British BIDs – the representative group for Business
Improvement Districts – said the report showed that maintaining a 2-metre
distance was “hugely problematic”.
“There’s a real
sense that the government is making it up as it goes along,” he said.
What’s the
issue?
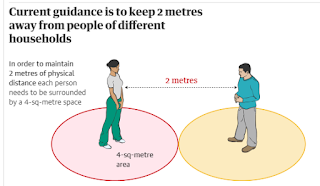
Have a look at the calculations on the diagrams. Here is the first one. What is going on here?
Each person is in a circle, radius 1 metre. So the area is π m2
Suggesting 4-sq-metres is therefore a bit strange.
That is, however, the area of a square with each person at its
centre. The square would be of side
2m. Maybe they assumed it was a
square? Maybe they have rounded up (despite
pi being closer to 3 than to 4)?
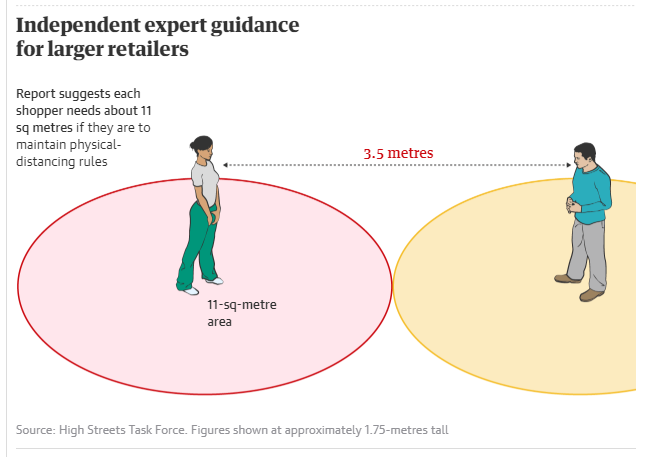
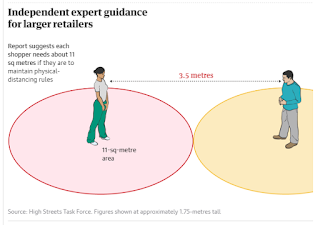
OK – now let’s look at the next diagram:
There’s no explanation here as to why each person now needs to be
in a circle with a radius of 1.75 metres.
This gives, apparently, an area of 11-sq-metres.
Well a circle of radius 1.75m has an area of about 9.6m2,
which doesn’t round up to give 11, so that theory was wrong. If this were a square for each person then it
would have sides of 3.5m, which dives an area of 12.25m2, which isn’t
11 either.
So are there two different errors here? Or something else entirely?
The original
report
I followed the link to the original report (https://www.highstreetstaskforce.org.uk/resources/details/?id=bc16b6bc-0ebb-4b7b-8df8-d8aa6b9a3a9f
) and found that some of it makes sense, some has been reported badly, and at
least one part of it is hilariously mathematically ridiculous.
Starting with the sensible part:
The research paper points out that when people move around a shop
they can’t stay exactly 2m away from everyone else. We see this at traffic lights. If you are four or five cars back when the
lights turn green, you can’t immediately start moving forwards. The first car moves, then the second driver
reacts to that movement, then the third car responds a little later, and it is
possible that the lights have turned red again before the tenth car has even
started moving. In a shop, if one person
stops to browse, or moves towards a display, those around are all affected and
need to respond. To account for this the
authors of the paper suggest a bigger circle is needed. And they go for a circle of radius 1.75m (more
on this later).
So that explains the bigger radius. But what about the two dodgy areas?
The Areas
The paper points out that circles don’t tessellate, so they use a ‘square
tessellation’. When arranged in this square formation, the total area divided
by the total number of people gives an area of 4m2 per person.
[Two diagrams (fig 4 and fig 6) from the paper.]
On the same diagrams I have shown the tessellations:
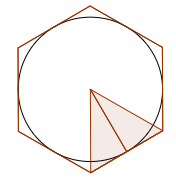
Later in the paper they mention the hexagonal tessellation. Let’s try that out with a circle of radius
1.75m
The hexagon goes around the edge of the circle, so the ‘height’ of
the shaded triangle is 1.75m. The base
is therefore 2 x 1.75 x tan30. When we
work out the area of this triangle and multiply by 6 (to find the area of the hexagon),
we get an answer of 10.6088112 m2.
Aha – that rounds off to 11 – and is presumably where that figure came
from!
What a shame that the article doesn’t explain this, and what a
shame their diagrams are so unclear.
But, I mentioned there are ridiculous things in the report as
well.
The first maths
error
Here is a quote from the report:
In square or
rectangular tessellations, the density of the circles is 0.7854 (Williams,
1979, p. 49). In other words, 78.5% of the space can be utilised.
Based on a
square tessellation, in fixed space each person will require a space of π(r)2/0.7894m2
(3.9797m2 when r = 1m) for the square or rectangular tessellation.
What is going on here? The
diagram shows the scenario, where a circle of radius 1 is inside a square,
which clearly has sides of length 2. The
area of the circle is π, and the area of the square is 4, so the fraction of
the area of the square that is taken up by circle is π ÷ 4 = 0.7853981634…
The book they are quoting uses a rounded version of this value
(0.7854) , which is where the figure of 78.5% of the space being filled comes
from.
Rather than just saying the area of the square is clearly 4, the
report then tries to divide the area of the circle by 0.7854 to get the area of
the square. This would give 3.999990646,
which is close to 4, but is a ridiculous way to do it!
Unfortunately, having written the correct rounded value of 0.7854
in the previous sentence, they then miscopy that in their calculations and
divide the area of the circle by 0.7894 instead, which gives 0.979722135,
and they have correctly rounded this off to 3.9797.
A nice bit of maths
(with another error)
Having done some bizarre things when working out the area of a
square of side 2m, there is then some nice maths to decide that a circle of
radius 1.75m is required.
They use a study of walking speeds in different environments (roughly
1.5m/s), and a different study that looked at how long it takes someone to stop
walking (0.5 seconds), worked out that this is therefore a stopping distance of
0.75m and that in order to stay 2m apart, that stopping distance of 0.75m
should be added on to each person’s circle.
The original radius of 1m, plus the stopping distance of 0.75m gives
1.75m.
This assumes an instantaneous deceleration and that everyone walks and
reacts in the same way. I think these are reasonable assumptions to make. Unfortunately, the formula they use to calculate
this extra amount is noted as this:
We set the value of x, the radius
of the inner circle giving freedom of movement, as walking speed / stopping
time.
It should be speed multiplied by stopping time.
This then gives them different areas required for different
sizes of shop, because people walk at different speeds in smaller shops
compared to larger ones and therefore the stopping distance is different.
What now
with this?
Unfortunately, this is another reason not to trust the maths
you see being used in the newspaper.
Rather disappointingly, there were basic errors in the news article
(which didn’t explain the whole square and hexagon thing), and in the
university report it was based on, which included multiple ridiculous things.
Perhaps worth using with a class to point out the folly of
applying a formula when you don’t need to, and the danger of rounding off too early?
Given how much of this is just twaddle, it seems appropriate to end with the last line of the original article:
“There’s a real sense that the government is making it up as it goes along,” he said.